Related Topics: Link to heading
“数组”: https://leetcode.com/tag/array/ “哈希表”: https://leetcode.com/tag/hash-table/ “二分查找”: https://leetcode.com/tag/binary-search/ “动态规划”: https://leetcode.com/tag/dynamic-programming/ Similar Questions: “长度最小的子数组”: https://leetcode.com/problems/minimum-size-subarray-sum/
Problem: Link to heading
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出:3
解释:
长度最长的公共子数组是 [3, 2, 1] 。
提示:
1 <= len(A), len(B) <= 10000 <= A[i], B[i] < 100
Solution: Link to heading
方法一:动态规划

class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(), m = nums2.size();
int ans = 0;
vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
for (int i = n-1; i >=0; i--){
for (int j = m-1; j >=0; j--){
dp[i][j] = nums1[i]==nums2[j] ? dp[i + 1][j + 1] + 1 : 0;
ans = max(ans, dp[i][j]);
}
}
return ans;
}
};
复杂度分析
- 时间复杂度: $O(N \times M)$ 。
- 空间复杂度: $O(N \times M)$ 。
方法二:滑动窗口
思路及算法
我们注意到之所以两位置会比较多次,是因为重复子数组在两个数组中的位置可能不同。以 A = [3, 6, 1, 2, 4], B = [7, 1, 2, 9] 为例,它们的最长重复子数组是 [1, 2],在 A 与 B 中的开始位置不同。
但如果我们知道了开始位置,我们就可以根据它们将 A 和 B 进行「对齐」,即:
A = [3, 6, 1, 2, 4] B = [7, 1, 2, 9] ↑ ↑ 此时,最长重复子数组在 A 和 B 中的开始位置相同,我们就可以对这两个数组进行一次遍历,得到子数组的长度,伪代码如下:
ans = 0
len = min(A.length, B.length)
k = 0
for i in [0 .. len - 1] do
if (A[i] == B[i]) then
k = k + 1
else
k = 0
end if
ans = max(ans, k)
end for
注意这里指定了 A[i] 对齐 B[i],在实际代码实现中会通过指定初始位置 addA 与 addB 的方式来对齐,因此表达式会略有差别。
我们可以枚举 A 和 B 所有的对齐方式。对齐的方式有两类:第一类为 A 不变,B 的首元素与 A 中的某个元素对齐;第二类为 B 不变,A 的首元素与 B 中的某个元素对齐。对于每一种对齐方式,我们计算它们相对位置相同的重复子数组即可。
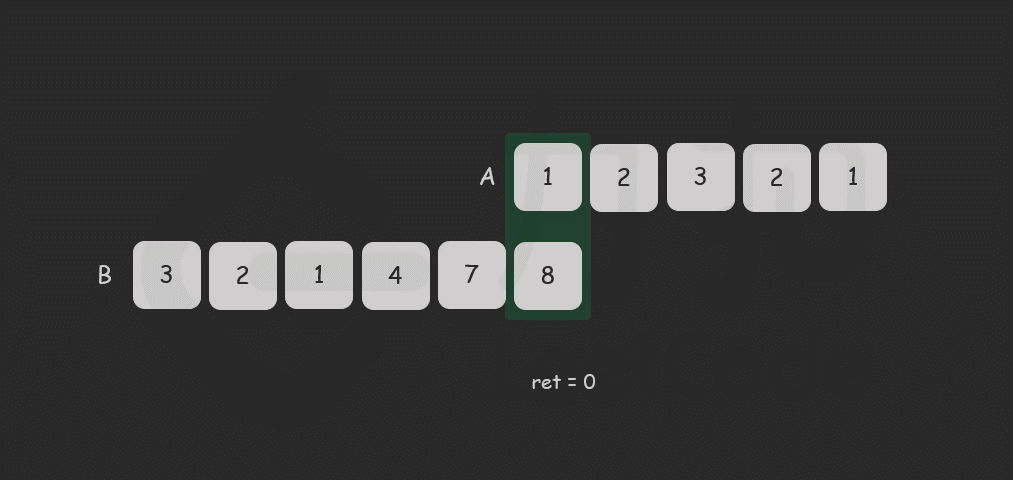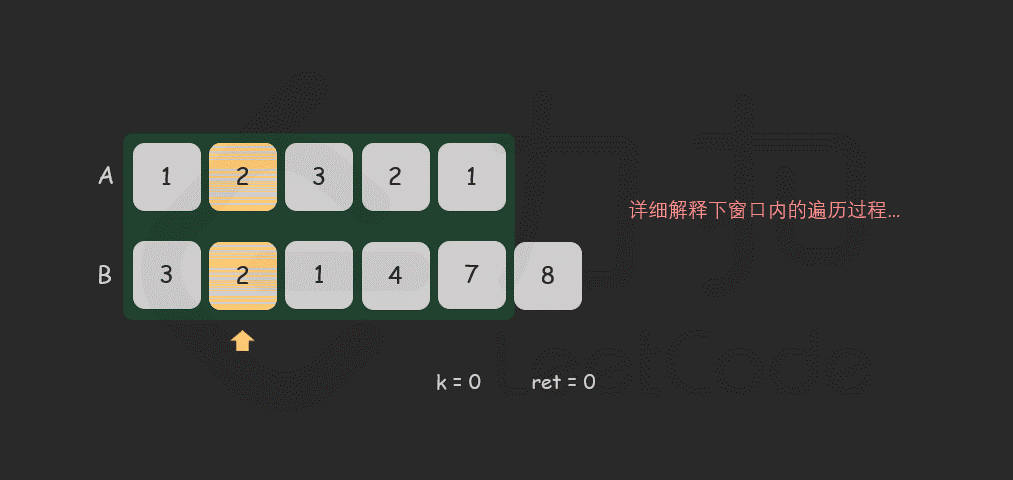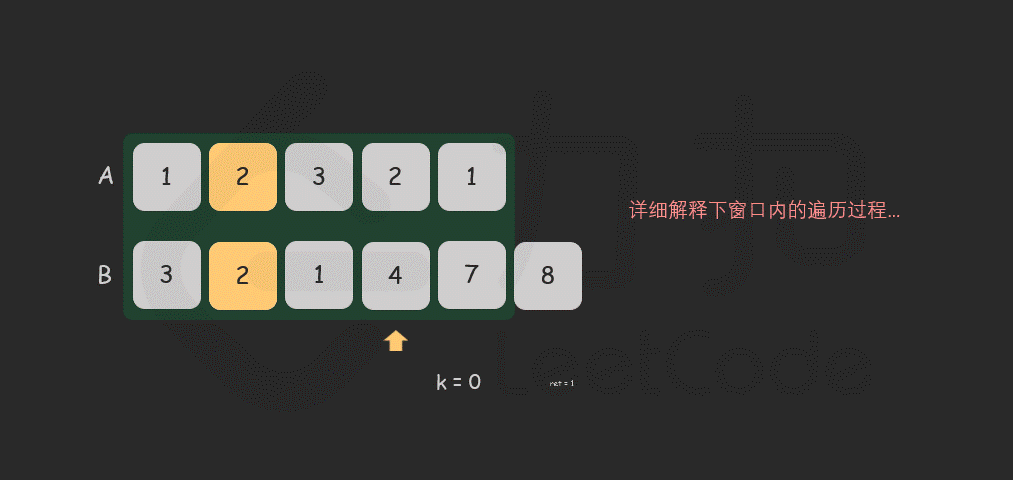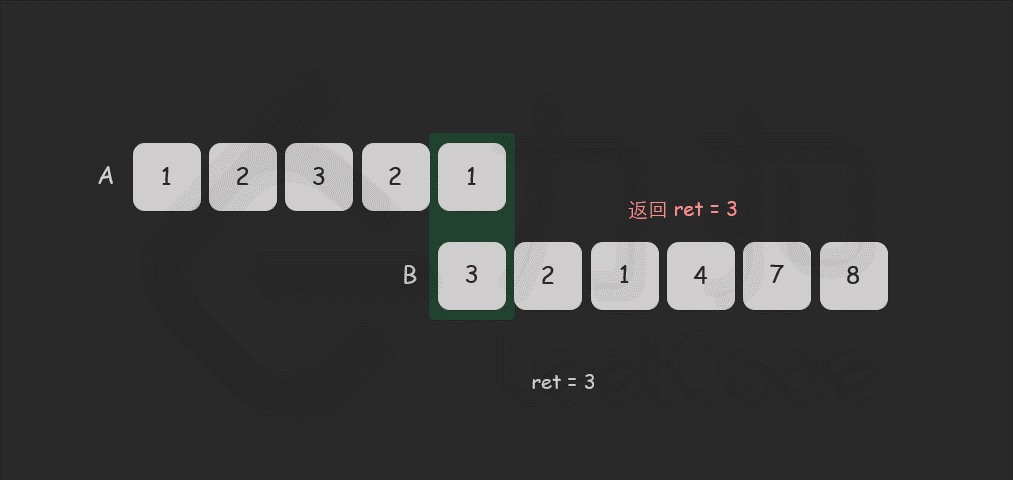
代码
class Solution {
public:
int maxLength(vector<int>& A, vector<int>& B, int addA, int addB, int len) {
int ret = 0, k = 0;
for (int i = 0; i < len; i++) {
if (A[addA + i] == B[addB + i]) {
k++;
} else {
k = 0;
}
ret = max(ret, k);
}
return ret;
}
int findLength(vector<int>& A, vector<int>& B) {
int n = A.size(), m = B.size();
int ret = 0;
for (int i = 0; i < n; i++) {
int len = min(m, n - i);
int maxlen = maxLength(A, B, i, 0, len);
ret = max(ret, maxlen);
}
for (int i = 0; i < m; i++) {
int len = min(n, m - i);
int maxlen = maxLength(A, B, 0, i, len);
ret = max(ret, maxlen);
}
return ret;
}
};
复杂度分析 时间复杂度: $O((N+M) \times \min (N, M))$ 。 空间复杂度: O(1)。 $\begin{array}{l}\mathrm{N} \text { 表示数组 } \mathrm{A} \text { 的长度, } & \text { M } \text { 表示数组 } \mathrm{B} \text { 的长 }\end{array}$
方法三:二分查找 + 哈希
思路及算法
如果数组 A 和 B 有一个长度为 k 的公共子数组,那么它们一定有长度为 j <= k 的公共子数组。这样我们可以通过二分查找的方法找到最大的 k。
而为了优化时间复杂度,在二分查找的每一步中,我们可以考虑使用哈希的方法来判断数组 A 和 B 中是否存在相同特定长度的子数组。
注意到序列内元素值小于 100 ,我们使用 Rabin-Karp 算法来对序列进行哈希。具体地,我们制定一个素数 base,那么序列 S 的哈希值为:

在二分查找的每一步中,我们使用哈希表分别存储这两个数组的所有长度为 len 的子数组的哈希值,将它们的哈希值进行比对,如果两序列存在相同的哈希值,则认为两序列存在相同的子数组。为了防止哈希碰撞,我们也可以在发现两个子数组的哈希值相等时,进一步校验它们本身是否确实相同,以确保正确性。但该方法在本题中很难发生哈希碰撞,因此略去进一步校验的部分。
代码
class Solution {
public:
const int mod = 1000000009;
const int base = 113;
// 使用快速幂计算 x^n % mod 的值
long long qPow(long long x, long long n) {
long long ret = 1;
while (n) {
if (n & 1) {
ret = ret * x % mod;
}
x = x * x % mod;
n >>= 1;
}
return ret;
}
bool check(vector<int>& A, vector<int>& B, int len) {
long long hashA = 0;
for (int i = 0; i < len; i++) {
hashA = (hashA * base + A[i]) % mod;
}
unordered_set<long long> bucketA;
bucketA.insert(hashA);
long long mult = qPow(base, len - 1);
for (int i = len; i < A.size(); i++) {
hashA = ((hashA - A[i - len] * mult % mod + mod) % mod * base + A[i]) % mod;
bucketA.insert(hashA);
}
long long hashB = 0;
for (int i = 0; i < len; i++) {
hashB = (hashB * base + B[i]) % mod;
}
if (bucketA.count(hashB)) {
return true;
}
for (int i = len; i < B.size(); i++) {
hashB = ((hashB - B[i - len] * mult % mod + mod) % mod * base + B[i]) % mod;
if (bucketA.count(hashB)) {
return true;
}
}
return false;
}
int findLength(vector<int>& A, vector<int>& B) {
int left = 1, right = min(A.size(), B.size()) + 1;
while (left < right) {
int mid = (left + right) >> 1;
if (check(A, B, mid)) {
left = mid + 1;
} else {
right = mid;
}
}
return left - 1;
}
};